Как найти формулу дельта лямбда

Дельта — буква, знак и его происхождение, применение в науке

В данной статье поговорим о знаке Дельта — что он из себя представляет, в каких сферах применяется и для чего вообще используется. Также вы узнаете, как выглядит знак и как его можно вставить в текст в такой программе, какой является Ворд из Майкрософт Оффис.

Знак Дельта применяется во многих сферах жизнедеятельности, к примеру, в физике, текстовых редакторах, формулах и других сферах. Чаще всего именно при печати учебной литературы, докладов и других видов документов применяют знак дельта, который имеется в разных версиях ВОРД от Виндовс и других приложениях для создания документов текстового формата на ПК.

О происхождения знака

Появление символа связано с греческими языком, но сама буква появилась от стародревнего финийского языка, в котором именовалась – далет, что обозначало («вход в дверь»). Выглядела «далет» как перевернутый влево равнобедренный треугольник. В греческом алфавите, была такая буква. Позже эта буква дала начало всем известной буквы латинского набора – D , которая и поныне есть во многих алфавитных рядах разных государств мира, к примеру, английский алфавит ее содержит.

Буква, которая служит аналогом в русском алфавите – Д, а вот символ везде одинаков и изображается, как геометрическая фигура, а именно треугольник с равными сторонами (Δ). Эта версия является заглавной, прописная версия выглядит немного иначе, представляя собой кружок с хвостиком, похожий на обозначение в физике плотности (δ).

Где применяется данный символ?

Кроме использования в правописании греков, символ начали активно применять в математике, геометрии, алгебре, физике, химии и географии.

Поговорим отдельно о применении дельта в каждых научных сферах:

1. География. Дельта подразумевает в географическом смысле начальную часть реки, океана или моря, имеет смысловое, нежели символическое, буквенное понятие и восприятие. Почему именно область впадения реки принято так называть? Все просто, дело в форме данной области, если сделать снимок сверху, то отток реки будет иметь форму правильного треугольника, а символ дельта, как раз представляет собой такой геометрический объект. Ярчайшим представителем с выраженной дельтой является река Нил (Египет), которая впадает в Средиземное море, а также Амазонка с ее впадением в океан Атлантики.
2. Применение в математике, алгебре, геометрии. Очень часто знак применяют в математической сфере для таких целей, как: 1) Приращение аргумента подразумевает под дельтой измененную переменную. К примеру, сложим 5 и 4 в итоге получим число 9. Дельтой будет являться увеличение 5 на 4. 2) Применение в теории вероятности по системе Лапласа. Такой метод преподают в ВУЗах, а не школах и в нем используют такой знак. 3) А также символ применяется при обозначении прямой и обратной матриц. 4) Дельта, буква, применяемая в написании формул (как письменным методом, так и через компьютер);
3. Также в математике применяют прописную версию дельта. А именно, такой символ обозначает производную от числа. Обозначение выглядит следующим образом — δy/δx. 2) Используется для описания бесконечной функции-дельта. Бесконечная функция возможна, если все значения аргумента равны нулю. 3) При помощи δ еще обозначают символику Кронекера, символ равен всегда 1, при условии того, что все его индексы равны, либо нулевые при заданных условиях.
4. Физика, астрономия, космогония. Граничащие меж собой научные дисциплины, все особо важные и по-своему интересные, в каждой из дисциплин можно встретить знак дельта. В физике связь всех производных осуществляется при помощи формул с интеграцией. К примеру, формула скорости, которая выглядит следующим образом — δS к δt , является отношением одной части к другой. В данном случае расстояние, которое преодолел объект, соотносится со временем, затраченном на преодоление. Вторая производная – это ускорение, где тоже важна взаимосвязь одной составляющей формулы к другой. В космологии и астрономии применяют формулы, расчеты с данным символом, только в прописном варианте.

Как ввести в «Ворд»?

Для вставки символа заходим в верхние меню редактора и ищем колонку «Вставка», наводим на колонку курсором мыши без нажатия правой кнопки. Высвечивается несколько наименования разделов, необходимо нажать на «Символ» , где можно путем перелистывания за счет колеса мыши искать необходимый знак, либо в строке поиска выбрать категорию (статистические или математические) и найти знак. Прописной или заглавный символ высветится в рабочей области окна вставки , вам только стоит нажать правой кнопкой мыши «вставить» или «окей».

Использование [ править | править код ]

Прописная буква Δ используется как символ для обозначения:

• изменения или различия между значениями переменных (например, температуры: ΔT), обычно конечного;
• дифференциальногооператора Лапласа;
• любой из дельта-частиц в физике элементарных частиц;
• в электронике существует ΔΣ-модуляция;
• 4-й квадры в соционике;
• Плотность заряжания во внутренней баллистике.

Строчная буква δ используется как символ для обозначения:

• малого изменения значения переменной, точнее — обозначение неполного дифференциала (или вариации), в отличие от полного, обычно обозначаемого латинской буквой d;
• символа Кронекера в точных науках;
• G-дельта-множество;
• дельта-функции Дирака в математике;
• отклонения в инженерной механике;
• коэффициент общей полноты (в судостроении)
• в астрономии

• четвёртая по яркостизвезда в созвездии;
• одна из двух небесных координат — склонение

химический сдвиг (ядерный магнитный резонанс).
удаления при читке корректуры (используется ещё с классических времён).

Определение дельты лямбды

Дельта лямбда может использоваться в различных областях знания, от математики и физики до экономики и программирования. Она помогает разобраться в изменении значения параметра и оценить его влияние на результаты расчетов.

Расчет дельты лямбды производится путем вычитания конечного значения параметра λ из начального значения. Полученное значение может быть как положительным, так и отрицательным, в зависимости от характера изменений.

Для формального определения дельты лямбды используется следующая формула:

Δλ = λконечное — λначальное

Например, для функции y = 2x + 3, где λ — это переменная x, можно рассчитать дельту лямбды по следующим шагам:

1. Выбрать начальное значение для переменной x, например xначальное = 0.
2. Вычислить значение функции при выбранном начальном значении, используя формулу y = 2x + 3. В данном случае yначальное = 3.
3. Выбрать конечное значение для переменной x, например xконечное = 5.
4. Вычислить значение функции при выбранном конечном значении, используя формулу y = 2x + 3. В данном случае yконечное = 13.
5. Рассчитать дельту лямбды по формуле Δλ = λконечное — λначальное: Δx = 5 — 0 = 5.

Таким образом, в данном примере дельта лямбда равна 5.

Some practical examples of dubious use 😉

You are in orbit around Earth, at the altitude of the International Space Station: you want to reach the Moon. How much fuel do you need to get there?

We plan on using a Hohmann transfer, a set of two burns described by this sequence:

• The departure from a circular orbit;
• The first burn, that accelerates the vehicle from the circular orbit to an elliptic one, at its perigee;
• The coasting phase;
• The second burn to transfer the vehicle on the target circular orbit from the apogee of the elliptic one by changing its speed to match the circular orbit’s one;
• The destination: a circular orbit with a larger radius.

The delta-v of a maneuver depends on the trajectory the vehicle will follow. There are many types of maneuvers, with different values of delta-v. The Hohmann transfer is generally a good choice in terms of efficiency, but it’s not necessarily the best one!

The first circular orbit, at 400 km of height over the surface of Earth, requires a speed of about vc1=7.67 kmsv_{\text{c}_1} =7.67\ \text{km}/\text{s}vc1​​=7.67kms — you can calculate the orbital speeds by using our orbital velocity calculator.

The transfer orbit, with an elliptic shape, has two characteristic velocities:

• Velocity at the perigee (velliptic)p=10.76 kms(v_\text{elliptic})_p=10.76\ \text{km}/\text{s}(velliptic​)p​=10.76kms, higher than the one in the circular orbit;
• Velocity at the apogee (velliptic)a=1.82 kms(v_\text{elliptic})_a =1.82\ \text{km}/\text{s}(velliptic​)a​=1.82kms, lower than the one of the target orbit.

The final orbit is circular, at a distance of about 40, ⁣000 km40,\!000\ \text{km}40,000km. The corresponding orbital velocity is about 1 kms1\ \text{km}/\text{s}1kms.

It is straightforward to calculate the required delta-v in both burn:

• Δv1=3.09 kms\Delta v_1 = 3.09\ \text{km}/\text{s}Δv1​=3.09kms
• Δv2=0.82 kms\Delta v_2 = 0.82\ \text{km}/\text{s}Δv2​=0.82kms

Which sum to a total delta-v of Δv=Δv1+Δv2=3.91 kms\Delta v= \Delta v_1 + \Delta v_2 = 3.91\ \text{km}/\text{s}Δv=Δv1​+Δv2​=3.91kms.

Let’s now take the parameters of a classic rocket engine, the third stadium of the Saturn V, which moved the Apollo spacecraft on the lunar transfer orbit in real life. We are going to use it for both burns.

The engine has a specific impulse of 421 s421\ \text{s}421s in the vacuum (where it will be used). Then we consider the dry mass of the Apollo craft, assuming we are going to reach the Moon by tapping into the fuel reserve. The value is 11, ⁣900 kg11,\!900\ \text{kg}11,900kg.

Input all of these values in the calculator, with the final mass of the spacecraft as mtm_tmt​. The resulting initial mass mm_0m​ is about 31, ⁣000 kg31,\!000\ \text{kg}31,000kg, almost three times the mass of the dry capsule. This is a lot of fuel!

The vast majority of our delta-v budget is usually spent on escaping the gravity attraction of Earth. As we explained, the Δv\Delta vΔv required to reach a low Earth orbit is about 9 kms9\ \text{km}/\text{s}9kms — compare it with the 4 kms4\ \text{km}/\text{s}4kms needed to reach the Moon! Once we are far enough from this possessive planet, the amount of fuel required is never excessive!

Let’s go the other way. Let’s assume you are aboard a rocket equipped with a NERVA engine, a colossal nuclear-powered engine studied in the ’70s. The specific impulse of that beast was Isp=841 sI_{sp}=841\ \text{s}Isp​=841s. Your spacecraft weights 40 t40\ \text{t}40t, and you loaded a mere 20 t20\ \text{t}20t of fuel — and you are going to use it all. We suppose that it will be enough for quite a journey with that engine!

We calculate the delta-v with the rocket equation:

Δv=841 s⋅9.81 ms2⋅ln⁡(60, ⁣00040, ⁣000)=3.345 kms\begin{align*}
\Delta v & = 841\ \text{s} \cdot 9.81\ \frac{\text{m}}{\text{s}^2} \cdot \ln\left({\frac{60,\!000}{40,\!000}}\right) \\
& = 3.345\ \text{km}/\text{s}
\end{align*}Δv​=841s⋅9.81s2m​⋅ln(40,00060,000​)=3.345kms​

Формула расчета дельты m

Дельта m (△m) является разностью масс между двумя состояниями системы (начальным и конечным). Эта величина позволяет определить изменение массы в химической реакции, физическом процессе или других контекстах, где требуется измерение изменения массы.

Формально, формулу расчета дельты m можно записать следующим образом:

где:

• m_{начальное} — масса в начальном состоянии системы;
• m_{конечное} — масса в конечном состоянии системы;
• △m — изменение массы системы.

Иногда △m может быть положительным или отрицательным числом, в зависимости от направления изменения массы системы. Положительное значение △m указывает на увеличение массы, а отрицательное значение — на уменьшение массы.

Примеры использования формулы расчета дельты m приведены ниже:

1. Взвешивание реагентов до и после химической реакции для определения степени протекания реакции.
2. Измерение потери массы при испарении жидкости.
3. Определение массы продуктов взрыва.
4. Расчет потерь массы в системе из-за окисления материала.

Формула расчета дельты m является универсальным инструментом для измерения изменения массы в различных контекстах и играет важную роль в науке, технике и промышленности.

Как найти значение дельты m в химической реакции

Дельта m, или изменение массы, является важным параметром в химических реакциях, позволяющим определить количество вещества, принимающего участие в реакции. Дельта m может быть положительной, если масса продуктов реакции больше массы исходных веществ, или отрицательной, если масса уменьшается.

Для расчета дельты m необходимо учитывать коэффициенты стехиометрического уравнения реакции, указывающие на количество вещества, участвующего в реакции. Для удобства расчета дельты m можно использовать таблицу с химическими элементами и их относительными атомными массами.

Процедура расчета дельты m следующая:

1. Записать уравнение химической реакции.
2. Определить количество вещества исходных веществ (обычно указывается в условии задачи или можно посчитать на основе данных о массе и атомных массах элементов).
3. Умножить количество вещества каждого исходного вещества на его молекулярную массу.
4. Сложить полученные значения для всех исходных веществ, чтобы получить общую массу исходных веществ.
5. Аналогично определить общую массу продуктов реакции, учитывая коэффициенты стехиометрического уравнения.
6. Вычислить разницу между общей массой продуктов и общей массой исходных веществ. Если разница положительная, то дельта m будет положительной, если отрицательная — дельта m будет отрицательной.

Пример расчета:

Исходные вещества: 2H₂ + O₂

Продукты реакции: 2H₂O

Вещество	Молекулярная масса (г/моль)	Количество вещества (моль)	Масса (г)
2H2	2 * 2.016 = 4.032	1	4.032
O2	2 * 16.00 = 32.00	1	32.00
2H2O	2 * 18.02 = 36.04	2	72.08
	Исходные вещества:	36.032
	Продукты реакции:	72.08
	Дельта m:	72.08 — 36.032 = 36.048

Таким образом, значение дельта m в данной реакции равно 36.048 г.

След в растяжках тела

Это конечное расширение поля , тогда трек представляет собой линейную карту после . Если понимать как -векторное пространство, то след элемента определяется как след матрицы представления -линейного эндоморфизма . Если — Галуа , след элемента можно представить как сумму его сопряженных элементов:
Л.K{\ displaystyle L / K}K{\ displaystyle K}Л.{\ displaystyle L}K{\ displaystyle K}Л.{\ displaystyle L}K{\ displaystyle K}α∈Л.{\ displaystyle \ alpha \ in L}K{\ displaystyle K}Л.∋Икс↦α⋅Икс∈Л.{\ Displaystyle L \ ni х \ mapsto \ alpha \ cdot x \ in L}Л.K{\ displaystyle L / K} α∈Л.{\ displaystyle \ alpha \ in L}

ТрЛ.K⁡(α)знак равно∑σ∈Гал⁡(Л.K)σ(α){\ displaystyle \ operatorname {Tr} _ {L / K} (\ alpha) = \ sum _ {\ sigma \ in \ operatorname {Gal} (L / K)} \ sigma (\ alpha)}.

Примеры расчета дельты лямбды

Для наглядности рассмотрим несколько примеров расчета дельты лямбды:

Пример 1:

Пусть у нас есть два измерения показателя A: A₁ = 10 и A₂ = 15, и два измерения показателя B: B₁ = 5 и B₂ = 8.

Тогда формула для расчета дельты лямбды будет выглядеть следующим образом:

Δλ = (B₂ — B₁) / (A₂ — A₁)

Подставляем известные значения:

Δλ = (8 — 5) / (15 — 10) = 3 / 5 = 0.6

Пример 2:

Пусть теперь у нас есть измерения показателя C: C₁ = 20 и C₂ = 25, и измерения показателя D: D₁ = 10 и D₂ = 15.

Тогда формула для расчета дельты лямбды будет выглядеть так:

Δλ = (D₂ — D₁) / (C₂ — C₁)

Подставляем известные значения:

Δλ = (15 — 10) / (25 — 20) = 5 / 5 = 1

Таким образом, в примере 1 дельта лямбда равна 0.6, а в примере 2 — 1.

Расчет дельты лямбды позволяет определить изменение значения показателей в различных условиях и использовать эту информацию для принятия решений в различных областях.

Определение дельты m

Дельта m — это символ, используемый в физике для обозначения изменения массы. Он часто используется при расчетах, чтобы показать разницу между начальной и конечной массой объекта или системы.

В математике дельта часто представлена большой буквой греческого алфавита Δ. Когда речь идет о массе, дельта m означает изменение массы и может быть выражена в килограммах, граммах или других единицах измерения массы.

Дельта m выражает разницу между двумя значениями массы и может быть положительным или отрицательным числом. Если дельта m положительна, это означает, что масса увеличилась. Если дельта m отрицательна, это указывает на уменьшение массы.

Чтобы найти дельту m, необходимо знать начальную и конечную массу объекта или системы.

Математически дельта m можно выразить следующим образом:

Δm = m_{конечная} — m_{начальная}

Например, если начальная масса объекта составляет 100 г, а конечная масса составляет 150 г, то дельта m будет равна 150 г минус 100 г, что дает нам 50 г.

Дельта m полезна при расчетах изменений массы в различных физических и химических процессах, таких как испарение, сгорание и химические реакции.

Символы вероятности и статистики

Закон Гесса

Аддитивность теплот реакций вытекает непосредственно из первого закона термодинамики: изменение энергии или энтальпии между двумя состояниями системы зависит только от самих этих состояний, а не от того, каким образом осуществляется переход между ними. Следовательно, разность между энтальпиями реагентов и продуктов, т.е теплота реакции, должна зависеть только от исходного и конечного состояний, а не от того конкретного пути, по которому следует реакция. Это утверждение носит название закон аддитивности теплот реакций (закон Гесса).

Благодаря закону Гесса совсем не обязательно измерять изменение энтальпии каждой возможной химической реакции. Например, если известны теплота испарения жидкой воды (3), то совсем не обязательно измерять теплоту разложения пероксида водорода с образованием водяного пара; эту величину гораздо проще получить путем вычислений. Если какую-либо реакцию трудно провести в лабораторных условиях, можно попытаться подобрать последовательность легче осуществляемых реакций, сумма которых дает необходимую реакцию. После измерения изменений энтальпии для всех индивидуальных реакций в такой последовательности можно просуммировать соответствующие изменения энтальпии подобно самим химическим уравнениям и найти теплоту трудно проводимой реакции.

Урок 19 «Изменение энтальпии» бесспорно был сложным, но чрезвычайно важным. Скорее всего у вас сейчас каша в голове, но не пугайтесь, ведь в следующем уроке все встанет на свои места. Если у вас возникли вопросы по данному уроку, то пишите их в комментарии.

Эволюция коронавируса

Ученые могут наблюдать эволюцию вируса в реальном времени и пытаются описать, как эта эволюция может повлиять на наш иммунитет и, в дальнейшем, на лечение и вакцины. Здесь мы делимся всем, что знаем о вариантах COVID-19 и различных эзотерических способах, которыми ученые обсуждают мутации и эволюцию.

Ученые и исследователи выявляют мутации путем секвенирования SARS-CoV-2, выделенного от пациентов, просматривая все 30 000 букв его генома. Они сравнивают это с самыми ранними зарегистрированными вирусами, обнаруженными в Ухане и наблюдают за изменениями.

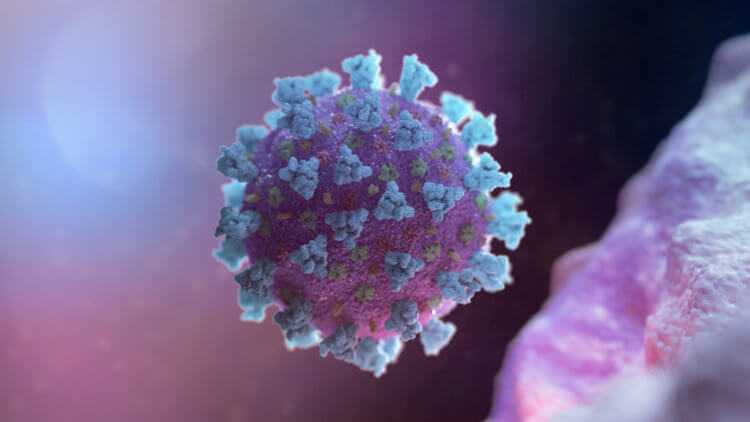
Каждая частица SARS-CoV-2 покрыта шипами. Проникновение в клетку требует, чтобы клубообразные выступы фиксировались на белке на поверхности человеческой клетки, известном как ACE2, что облегчает проникновение вируса.

Если исследователи увидят, что мутация становится все более распространенной в популяции, есть вероятность, что она изменила характеристики SARS-CoV-2. Любые мутации в геноме коронавируса приводят к вариантам вируса, но некоторые из них вызывают больше беспокойства, чем другие.

Chem – How to Calculate ΔH (Delta H) Part 3

December 6th, 2011 |
Author:

HOW DO YOU CALCULATE ΔH (DELTA H)?

Once you memorized the relationship between the side the energy is on in a chemical equation, the Δ H and endothermic or exothermic, you are probably curious about how Δ H is calculated. It is calculated by the total energy contained in the molecules of products minus the total energy of the molecules in the reactants. Any time you are calculating the Δ of something it is always FINAL – INITIAL. Another way to say that is FINISH – START or PRODUCTS – REACTANTS. The formula is below.

Energy of products – Energy of reactants = Δ H

But how do we count the energy of the products or the energy of the reactants? It turns out that each chemical has an energy associated with it. Just like you would read the amount of calories off the back of a food label. You can also find tables where you can look up the energy of different chemicals. Where do we get the energy of the individual chemicals? Here is a link to the place where you find the enthalpy (energy) of each chemical. It is referred to in chemistry as the Δ H_f  or the ENTHALPY OF FORMATION. REMEMBER to make sure the chemicals you look up also have the correct states of matter. If you want to find it in a chemistry text book, then it will usually be in the very back of the book in the index section.

VIDEO Calculate Δ H (DELTA H) Demonstrated Example 1: Use the balanced chemical equation below and calculate its Δ H. (Use this link look up the Δ H_f values)

CH_4(g) + 2 O_2(g) —-> CO_2(g) + 2 H₂O_(g)

What is the energy of the molecules of the products?

Answer: CO_2(g) = -394 kJ/mol H₂O_(g) = -242 kJ/mol

Do any of the molecules in the products have any coefficients?

Answer: Yes, H₂O_(g) 2 H₂O_(g) = 2 * (-242 kJ/mol)

What is the energy of the molecules of the reactants?

Answer: CH_4(g) = -75 kJ/mol O_2(g) = 0

Do any of the molecules in the reactants have any coefficients?

Answer: Yes, O_2(g) 2 O_2(g) = 2 * (0)

What is the general formula for Δ H?

Answer: Energy of products – Energy of reactants = Δ H

Modify the Δ H equation for this chemical equation.

(CO_2(g) + 2 H₂O_(g)) – (CH_4(g) + 2 O_2(g)) = Δ H

Fill in the numbers for this specific equation.

(-394 + 2 * (-242)) – (-75 + 2 * (0)) = Δ H

Solve for Δ H

COMPLETE ANSWER: Δ H = -803 kJ/mol

VIDEO Calculate Δ H (DELTA H) Demonstrated Example 2: Use the Δ H and balanced chemical equation below and calculate the Δ H_f of H₂Ba_(s). (Use this link look up the Δ H_f values)

2 NaH_(g) + BaCl_2(s) —-> H₂Ba_(s) + 2 NaCl_(s)Δ H = -536 kJ/mol

What is the energy of the molecules of the products?

Answer: H₂Ba_(s) = X kJ/mol NaCl_(s) = -411 kJ/mol

Do any of the molecules in the products have any coefficients?

Answer: Yes, NaCl_(s) 2 NaCl_(s) = 2 * (-411 kJ/mol)

What is the energy of the molecules of the reactants?

Answer: NaH_(g) = -55 kJ/mol BaCl_2(s) = -858 kJ/mol

Do any of the molecules in the reactants have any coefficients?

Answer: Yes, NaH_(g) 2 NaH_(g) = 2 * (-55 kJ/mol)

What is the general formula for Δ H?

Answer: Energy of products – Energy of reactants = Δ H

Modify the Δ H equation for this chemical equation.

(H₂Ba_(s) + 2 NaCl_(s)) – (2 NaH_(g) + BaCl_2(s)) = Δ H

Fill in the numbers for this specific equation.

( X + 2 * (-411)) – (2 * (-55) + -858) = -536

Solve for X

COMPLETE ANSWER: Δ H_f of H₂Ba_(s) = -682 kJ/mol

PRACTICE PROBLEMS: Calculate the Δ H or the Δ H_f as needed. (Use this link look up the Δ H_f)

Use the balanced chemical equation below and calculate its Δ H.

2 H₂O_(g) —-> 2 H_2(g) + O_2(g)

Answer: Δ H = +484 kJ/mol

Use the balanced chemical equation below and calculate its Δ H.

3 CaSO_4(s) + 2 Al(OH)_3(s) —-> 3 Ca(OH)_2(s) + Al₂(SO₄)_3(s)

Answer: Δ H = 462 kJ/mol

Use the Δ H and the balanced chemical equation below and calculate the Δ H_f of F–_(g).

H+_(g) + F–_(g) —-> HF_(g)Δ H = – 150 kJ/mol

Answer: Δ H_f of F–_(g) = -120 kJ/mol

Use the Δ H and balanced chemical equation below and calculate the Δ H_f of CN_(s).

2 HCN_(g) + AgCN_(s) —-> Ag_(s) + H_2(g) + 3 CN_(s)Δ H = -113 kJ/mol

Answer: Δ H_f of CN_(s) = 101 kJ/mol (do not forget to divide by the 3 coefficient)

Posted in Chemistry

Новые варианты COVID-19

Коронавирус SARS-CoV-2 постоянно эволюционировал с тех пор, как был впервые обнаружен у людей более года назад. Вирусы размножаются чрезвычайно быстро, и каждый раз, когда это происходит, есть небольшой шанс, что они мутируют. Это нормально. Особенно, если вы вирус.

Но в последние несколько недель ученые исследовали варианты SARS-CoV-2 с несколькими мутациями, возникающими гораздо быстрее, чем ожидалось. Обычно каждые несколько месяцев в коронавирусе наблюдаются от одного до двух в значительной степени несущественных генетических изменений. Появляются новые варианты с целым рядом мутаций, все в одно и то же время. В декабре 2020 года Великобритания объявила о варианте коронавируса, а два других варианта позже были обнаружены в Южной Африке и Бразилии. Ученые внимательно следят за появлением новых штаммов и оценивают их, потому что они могут усугубить пандемию.

Основные задачи вируса – распространение и выживание.

Эпидемиологам, вирусологам и иммунологам теперь поручено понять, как эти мутации в новых вариантах могут изменить вирус и как наш организм реагирует на них. Мутации могут изменить SARS-CoV-2 таким образом, что он может даже избежать иммунного ответа, вызванного вакцинами. Предварительные исследования показывают, что существующие вакцины должны быть способны справиться с тремя наиболее опасными вариантами, но данные продолжают поступать.

Как найти дельта l в физике формула

Автор Ѐасим задал вопрос в разделе Домашние задания

Формула вычисления дельта L по физике и получил лучший ответ

Ответ от Анастасия Терентьевакак правило, дельта в физике чаще всего (а может даже и всегда) обозначает изменение чего – либо. L насколько я помню это длина. Значит дельта L обозначает изменение длины, и находится по формуле: L2 – L1

Буква греческого алфавита дельта
Δδ

◄	ΐ	Α	Β	Γ	Δ	Ε	Ζ	Η	Θ	►
◄	ΰ	α	β	γ	δ	ε	ζ	η	θ	►

Характеристики

Название
Δ: greek capital letter delta δ: greek small letter delta

Юникод
Δ: U+0394δ: U+03B4

HTML-код
Δ‎: Δ или
Δ δ‎: δ или
δ

UTF-16
Δ‎: 0x394δ‎: 0x3B4

URL-код

Δ: %CE%94δ: %CE%B4

Мнемоника
Δ: Δ δ: δ

Δ , δ (название: де́льта, греч. δέλτα ) — 4-я буква греческого алфавита. В системе греческой алфавитной записи чисел имеет числовое значение 4. Происходит от финикийской буквы

дельтаththis

Дельта-потенциал — Delta potential

Часть серии на
Квантовая механика
я ℏ ∂ ∂ т | ψ ( т ) ⟩ = ЧАС ^ | ψ ( т ) ⟩ > | psi (t) angle = > | psi (t) angle>

В квантовая механика то дельта-потенциал это потенциальная яма математически описывается Дельта-функция Дирака — а обобщенная функция. Качественно он соответствует потенциалу, который везде равен нулю, кроме единственной точки, где он принимает бесконечное значение. Это можно использовать для моделирования ситуаций, когда частица может свободно перемещаться в двух областях пространства с барьером между двумя областями. Например, электрон может почти свободно перемещаться в проводящем материале, но если две проводящие поверхности расположены близко друг к другу, граница раздела между ними действует как барьер для электрона, который можно аппроксимировать дельта-потенциалом.

Дельта-потенциальная яма — это предельный случай из конечная потенциальная яма, который получается, если сохранить произведение ширины ямы на постоянную потенциала, уменьшая ширину ямы и увеличивая потенциал.

В этой статье для простоты рассматривается только одномерная потенциальная яма, но анализ можно расширить до других измерений.