Момент инерции — формулировка, свойства и методы решения

Содержание

В момент инерции твердого тела относительно определенной оси вращения представляет его сопротивление изменению угловой скорости вокруг указанной оси. Он пропорционален массе, а также положению оси вращения, поскольку тело, в зависимости от его геометрии, может легче вращаться вокруг одних осей, чем других.

Представьте себе большой объект (состоящий из множества частиц), который может вращаться вокруг оси. Предположим, что сила действует F, приложенная по касательной к элементу массы Δm_я, который создает крутящий момент или момент, определяемый τ_сеть = ∑р_я Икс F_я. Вектор р_я позиция Δm_я(см. рисунок 2).

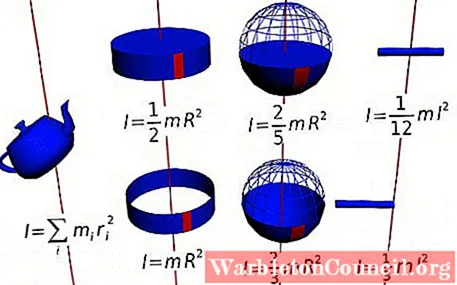
Этот момент перпендикулярен плоскости вращения (направление +k = выходит из бумаги). Поскольку сила и вектор радиального положения всегда перпендикулярны, поперечное произведение остается:

τ_сеть = ∑ F_я р_яk = ∑ (Δm_я к_я) р_я k = ∑ Δm_я (чтобы_я р_я ) k

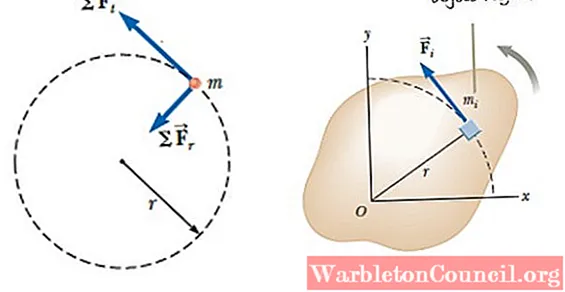
Разгон до_я представляет тангенциальную составляющую ускорения, поскольку радиальное ускорение не влияет на крутящий момент. В зависимости от углового ускорения α можно указать, что:

к_я = α r_я

Следовательно, чистый крутящий момент выглядит так:

 τ_сеть = ∑ Δm_я (α r_я2) k = (∑ р_я2 Δm_я)α k

Угловое ускорение α одинаково для всего объекта, поэтому на него не влияет индекс «i», и оно может оставлять суммирование, которое является в точности моментом инерции объекта, обозначенного буквой I:

I = ∑ r_я2 Δm_я

Это момент инерции дискретного распределения массы. При непрерывном распределении суммирование заменяется интегралом и Δm становится разницей масс дм. Интеграл проводится по всему объекту:

I = ∫_M(р2) дм

Единицы момента инерции в Международной системе СИ — кг x м.2. Это скалярная и положительная величина, так как это произведение массы и квадрата расстояния.

Момент инерции и его физический смысл

Обеспечить поступательное движение предмета при его толкании будет тем тяжелее, чем больше он весит. Аналогичные эксперименты предусматривались школьной программой и относились к прямо направленному действию.

Было понятно, что именно масса тела характеризует  степень его инертности и является ее мерой.

При совершении предметом вращательных движений наблюдается иной вид зависимости. В данном случае мерой инертности выступает момент инерции.

Момент инерции – скалярная измеряемая характеристика инертности тела в момент совершения осевого вращения.

https://youtube.com/watch?v=XwTGp_z3G9I

Задачи по определению величины момента инерции решаются с помощью теоремы Гюйгенса-Штейнера, смысл которой заключается в следующем:

МИ для тела, вращающегося вокруг какой-либо оси, равна сумме слагаемых единиц: момент инерции предмета, который вращается вокруг оси, параллельной данной, и проходящей через центр масс, а также произведения массы на расстояние между осями, возведенное в квадрат.

В приведенной формуле используются следующие обозначения: d – расстояние между осями, m – масса тела, Iz – момент инерции относительно рассматриваемой оси, а Ic – относительно оси, которая проходит через центр масс. В профильной литературе и учебниках буква I может заменяться J.

Формулировка способа количественного измерения момента инерции при осевом вращении предмета стала возможной в результате работы двух ученых-математиков: Гюйгенса и Штейнера. Теорема дает возможность быстрого решения задач на определение инерции предмета любой формы, для которого уже просчитана центробежная сила. Формула Штейнера позволяет вычислить момент инерции этого предмета относительно выбранной оси, проходящей параллельно прямой, следующей через центр фигуры.

Момент инерции твердого шара диаметром

Сферу радиуса R можно представить как набор дисков, установленных один на другой, причем каждый диск бесконечно малой массы дм, радио р и толщина дз, имеет момент инерции, определяемый:

 отдал_диск = (½) г2дм

Чтобы найти этот дифференциал, мы просто взяли формулу из предыдущего раздела и подставили M Y р от дм Y р, соответственно. Такой диск можно увидеть на фигуре 5.

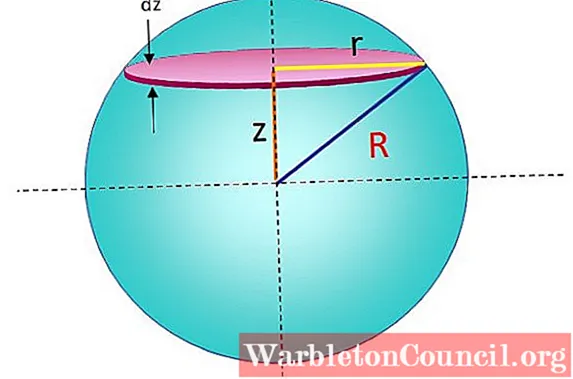
Путем сложения всех бесконечно малых моментов инерции уложенных друг на друга дисков получается полный момент инерции сферы:

я_сфера = ∫dI_диск

Что эквивалентно:

I = ∫_сфера (½) г2дм

Для решения интеграла необходимо выразитьдм должным образом. Как всегда, это достигается за счет плотности:

ρ = M / V = ​​dm / dV → dm = ρ.dV

Объем дифференциального диска составляет:

dV = Площадь основания x высота

Высота диска — это толщина дз, а площадь базы равна πr2, Таким образом:

 dV = πr2дз

А подставив в предложенный интеграл, он будет выглядеть так:

 I = ∫_сфера(½) г2dm = ∫ (½) r2(ρπr2дз)

Но перед интегрированием необходимо заметить, что r — радиус диска — зависит от z и R — радиуса сферы, как видно из рисунка 5. Используя теорему Пифагора:

р2 = г2 + z2 → г2 = R2 — г2

 Что приводит нас к:

 I = ∫_сфера(½) ρ r2(πr2dz) = ∫_сфера(½) ρ π r4дз= ∫_сфера(½) ρ π (R2 — г2)2 дз

Чтобы интегрировать по всей сфере, заметим, что z изменяется от –R до R, поэтому:

Знаю это ρ = M / V = ​​M / [(4/3) πR3] наконец, после упрощения получается:

Применяем второй закон Ньютона для вращательного движения

Согласно второму закону Ньютона (см. главу 5), ускорение объекта под действием силы пропорционально величине силы и обратно пропорционально массе объекта:

где ​\( \mathbf{a} \)​ — это вектор ускорения, \( \mathbf{F} \) — вектор силы, а ​\( m \)​ — масса объекта. Подробнее о векторах рассказывается в главе 4. Соблюдается ли этот закон для вращательного движения?

В главе 10 мы уже познакомились характеристиками вращательного движения, которые являются эквивалентами (аналогами) некоторых характеристик поступательного движения. А как будет выглядеть аналог у второго закона Ньютона? Похоже, что во вращательном движении роль ускорения \( \mathbf{a} \) играет угловое ускорение \( \alpha \), а роль силы \( \mathbf{F} \) — момент силы \( \mathbf{M} \)? Не вдаваясь в подробности, скажем лишь, что это действительно так. А что же с массой? Оказывается, что для этого используется новое понятие — момент инерции ​\( l \)​. Известно, что второй закон Ньютона для вращательного движения принимает следующий вид:

Рассмотрим простой пример. Пусть привязанный нитью мячик для игры в гольф вращается по окружности, как показано на рис. 11.1. Допустим, что к мячику приложена направленная по касательной к окружности тангенциальная сила, которая приводит к увеличению тангенциальной скорости мячика

(Обратите внимание, что речь идет не о нормальной силе, направленной вдоль радиуса окружности вращения. Более подробно нормальная и тангенциальная скорости, а также нормальное и тангенциальное ускорения рассматриваются в главе 10.)

Поскольку:

то, умножая обе части этой формулы на радиус окружности ​\( r \)​, получим:

Поскольку ​\( r\mathbf{F}=\mathbf{M} \)​ то

или

Таким образом, частично совершен переход от второго закона Ньютона для поступательного движения к его аналогу для вращательного движения. (Следует отметить, что это выражение справедливо для материальной точки, т.е. объекта, размерами которого можно пренебречь по сравнению с величиной радиуса окружности ​\( r \)​. Для протяженного объекта следует использовать другие формулы, которые описываются далее в этой главе. — Примеч. ред.)

Преобразуем тангенциальное ускорение в угловое

Чтобы полностью перейти от описания поступательного движения к описанию вращательного движения, необходимо использовать связь между угловым ускорением ​\( \alpha \)​ и тангенциальным ускорением ​\( \mathbf{a} \)​. Как нам уже известно из главы 10, они связаны следующим соотношением:

Подставляя это выражение в приведенную выше формулу

получим:

Итак, мы получили связь момента силы, действующей на материальную точку, и ее углового ускорения. Коэффициент пропорциональности между ними, ​\( l=mr^2 \)​, называется моментом инерции материальной точки. Таким образом, мы получили эквивалент второго закона Ньютона для вращательного движения, где роль силы играет момент силы, роль ускорения — угловое ускорение, а роль массы — момент инерции.

Пример: вычисляем момент силы для обеспечения углового ускорения

Если на объект действует несколько сил, то второй закон Ньютона имеет следующий вид:

где ​\( \mathbf{\sum\!F} \)​ обозначает векторную сумму всех сил, действующих на объект.

Аналогично, если на объект действует несколько моментов сил, то второй закон Ньютона имеет вид:

где \( \mathbf{\sum\! M} \) обозначает векторную сумму всех моментов сил, действующих на объект. Аналог массы, т.е. момент инерции, измеряется в кг·м2.

Пусть мячик из предыдущего примера (см. рис. 11.1) имеет массу 45 г, а длина нити равна 1 м. Какой момент сил необходимо приложить, чтобы обеспечить угловое ускорение — ​\( 2\pi с^{-2} \)​? Подставляя значения в уже известную нам формулу

получим:

Как видите, для решения этой задачи достаточно было поступить, как при определении силы, необходимой для обеспечения ускорения поступательного движения (где нужно было бы умножить массу на ускорение), т.е. умножить угловое ускорение на момент инерции.

Момент инерции цилиндра относительно оси, его основаниям перпендикулярной

Из приведенной выше формулы можно понять, что величина I является характеристикой всей вращающейся системы, то есть она зависит как от формы тела и распределения в нем массы, так и от относительного положения оси.

В данном пункте рассмотрим простой случай: определить необходимо момент инерции для сплошного цилиндра, ось вращения которого перпендикулярна его основаниям и проходит через гравитационный центр фигуры.

Для решения проблемы применим интегральную формулу для I. В процессе операции интегрирования мысленно разобьем цилиндр на тонкие колечки толщиной dr. Каждое колечко будет иметь объем: dV = 2*pi*r*dr*h, здесь h — высота фигуры. Учитывая, что dm = ρ*dV, где ρ — плотность цилиндра, получаем:

I = ∫r 2 dm = ρ*∫r 2 dV = 2*pi*ρ*h*∫r 3 dr

Этот интеграл необходимо вычислить для пределов от 0 до R, где R — радиус фигуры. Тогда получим:

I = 2*pi*ρ*h*∫ R r 3 dr = 2*pi*ρ*h/4*(r 4 )∣ R = pi*ρ*h*R 4 /2

Воспользовавшись формулой для массы цилиндра через его объем и плотность, приходим к конечному выражению:

I = m*R 2 /2, где m = pi*ρ*h*R 2

Мы получили формулу инерции момента цилиндра однородного. Она показывает, что величина I для этой фигуры в 2 раза меньше, чем для материальной точки аналогичной массы, которая вращается на расстоянии радиуса цилиндра от оси.

Примеры расчетов

Протяженный объект, например стержень, диск, сфера или другой, плотность которого ρ постоянна и зная, что плотность является отношением массы к объему, разность масс дм записывается как:

ρ = dm / dV → dm = ρdV

Подставляя в интеграл момент инерции, имеем:

 I = ∫r2 ρdV = ρ ∫r2dV

Это общее выражение, справедливое для трехмерного объекта, объем которого V и положение р являются функциями пространственных координат Икс, Y Y z

Обратите внимание, что, будучи постоянной, плотность находится вне интеграла

Плотность ρ она также известна как объемная плотность, но если объект очень плоский, как лист, или очень тонкий и узкий, как стержень, можно использовать другие формы плотности, давайте посмотрим:

— Для очень тонкого листа следует использовать плотность σ, поверхностную плотность (масса на единицу площади) и дает это разница площадей.

— А если это тонкий стержень, где важна только длина, используется линейная массовая плотность. λ и длина дифференциал, по отношению к оси, используемой в качестве ссылки.

В следующих примерах все объекты считаются жесткими (не деформируемыми) и имеют однородную плотность.

Пример решения задачи на нахождение момента инерции

Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.

Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.

Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:

Массу кольца можно представить в виде:

Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:

В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.

Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.

Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:

Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.

Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.

Геометрический момент инерции

Геометрический момент инерции — геометрическая характеристика сечения вида

где — расстояние от центральной оси до любой элементарной площадки относительно нейтральной оси .

Геометрический момент инерции не связан с движением материала, он лишь отражает степень жесткости сечения. Используется для вычисления радиуса инерции, прогиба балки, подбора сечения балок, колонн и др.

Единица измерения СИ — м 4 . В строительных расчетах, литературе и сортаментах металлопроката в частности указывается в см 4 .

Из него выражается момент сопротивления сечения:

Геометрические моменты инерции некоторых фигур
Прямоугольника высотой и шириной :
Прямоугольного коробчатого сечения высотой и шириной по внешним контурам и , а по внутренним и соответственно
Круга диаметром

Бизнес и финансы

БанкиБогатство и благосостояниеКоррупция(Преступность)МаркетингМенеджментИнвестицииЦенные бумагиУправлениеОткрытые акционерные обществаПроектыДокументыЦенные бумаги — контрольЦенные бумаги — оценкиОблигацииДолгиВалютаНедвижимость(Аренда)ПрофессииРаботаТорговляУслугиФинансыСтрахованиеБюджетФинансовые услугиКредитыКомпанииГосударственные предприятияЭкономикаМакроэкономикаМикроэкономикаНалогиАудитМеталлургияНефтьСельское хозяйствоЭнергетикаАрхитектураИнтерьерПолы и перекрытияПроцесс строительстваСтроительные материалыТеплоизоляцияЭкстерьерОрганизация и управление производством

Вычисление моментов инерции

Моментом инерции материальной точки относительно оси называется число , где — масса точки, а — ее расстояние от оси. Аналогично определяется момент инерции относительно точки.

Пусть — материальная линия, линейная плотность которой во всех точках равна единице. Тогда масса элементарного участка этой линии равна его длине , а момент инерции такого участка относительно оси абсцисс равен . Интегрируя, получаем момент инерции относительно оси абсцисс всей линии:

. Так же доказывается, что и ,

где — момент инерции относительно начала координат. Отсюда следует, в частности, что .

Если линия задана параметрическими уравнениями , то

Аналогичные формулы справедливы для и

Моменты инерции криволинейной трапеции

Перейдем к вычислению моментов инерции криволинейной трапеции. Будем считать, что ее поверхностная плотность равна единице. Сначала найдем момент инерции прямоугольника со сторонами и относительно стороны .

Разобьем его на элементарные прямоугольники со сторонами и (см. рис. 61). Площадь (а потому и масса) каждого такого прямоугольника равна .

Значит, момент инерции элементарного прямоугольника относительно стороны равен , а момент инерции всего прямоугольника относительно этой стороны выражается формулой

Аналогично доказывается, что момент инерции криволинейной трапеции относительно оси ординат выражается формулой

(момент инерции элементарного прямоугольника относительно оси ординат равен ).

Полярный момент инерции (т. е. момент относительно начала координат) в этом случае выражается формулой

Пример 9. Вычислить момент инерции равнобедренного треугольника относительно его основания.

Решение. Расположим оси координат так, как показано на рисунке 65.

Пусть основание треугольника , высота . Прямая проходит через точки и . Ее уравнение , то есть .

Ясно, что момент инерции треугольника относительно оси равен удвоенному моменту инерции треугольника относительно той же оси. Значит,

Как рассчитать момент инерции, формула

Измерение значения момента инерции можно произвести теоретически, согласно формуле. Для этого условно движущийся предмет разбивается на мелкие составляющие, масса которых обозначается  dm. В конечном итоге момент инерции (МИ) равняется сумме произведений всех образовавшихся масс на расстояние до оси, возведенное в квадрат.

Исходя из этой формулы, момент инерции, кроме массы тела, определяется положением оси, вокруг которой предмет вращается, а также его формой и габаритами.

Возможность рассчитать моменты инерции полезна, к примеру, при исследованиях свойств и структуры элементов Солнечной системы. Это так называемый безразмерный момент инерции. Высчитанная по формуле величина дает представление о распределении массы по глубине.

Момент инерции тонкого стержня относительно оси, проходящей через его центр

Здесь мы собираемся вычислить момент инерции тонкого, жесткого, однородного стержня длиной L и массой M относительно оси, проходящей через среду.

Во-первых, необходимо установить систему координат и построить фигуру с соответствующей геометрией, например:

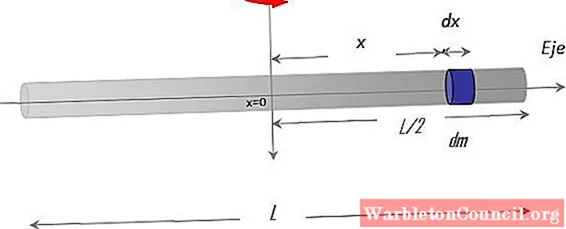
В Ось X вдоль бара и Ось y как ось вращения. Процедура определения интеграла также требует выбора разницы масс по стержню, называемой дм, имеющий дифференциальную длину dx и находится в позиции Икс произвольно, относительно центра х = 0.

Согласно определению линейной плотности массы λ:

λ = M / L

Поскольку плотность однородна, что верно для M и L, это также верно для dm и dx:

λ = dm / dx → dm = λdx.

С другой стороны, элемент массы находится в положенииИкс, то, подставляя эту геометрию в определение, мы получаем определенный интеграл, пределы которого являются концами стержня согласно системе координат:

Подставляя линейную плотность λ = M / L:

Чтобы найти момент инерции стержня по отношению к другой оси вращения, например, той, которая проходит через одну из своих крайних точек, вы можете использовать теорему Штейнера (см. Решенное упражнение в конце) или выполнить прямое вычисление, подобное показанному. здесь, но изменив геометрию соответствующим образом.

Формула инерции

В переводе с латыни инерция обозначает косность, вялость. В инерциальных системах отсчета тело стремится сохранить свое состояние покоя или равномерного прямолинейного движения без изменения, если на него не действуют другие тела или их действие взаимно компенсируется. Инерция – это свойство материи.

Мерой инерции служит масса. При вращательном движении в качестве меры инерции часто используют момент инерции.

Масса тела

• Масса является основной динамической характеристикой тела, выступает в качестве количественной характеристики его инертности, то есть возможности тела иметь определенное ускорение, которое придает ему сила. При этом для рассматриваемого тела ускорение () прямо пропорционально силе (), а коэффициент пропорциональности в данном случае это масса (m):
• И так, инертной массой называют физическую величину, равную частному от деления величины силы на модуль ускорения тела:

На сегодняшний момент пока нет четкого понимания, почему тела обладают массами, в чем состоит природа массы. Почему элементарные частицы обладают теми или иными массами. Однако определение массы в виде (2) дает возможность ее измерять. Кроме того, по найденной величине массы можно точно рассчитать движение того или иного тела. В чем и состоит основная задача механики.

1. Масса связана с таким параметром как количество вещества ():
2. где – молярная масса вещества.
3. При изучении движения тела следует учитывать не только совокупную массу тела, но и распределение масс в нем.
4. Следует заметить, что отношение силы к ускорению тела (2) , то есть масса, является постоянной величиной при относительно небольших скоростях. Если скорость тела увеличивается, то масса растет:
5. где m – релятивистская масса (или просто масса); – масса покоя; v – скорость движения тела; c – скорость света.

Момент инерции тела

• Инерцию тела во вращательном движении принято характеризовать при помощи такой физической величины как момент инерции тела (J). Момент инерции является скалярной (в общем случае тензорной) физической величиной, которую находят как сумму произведений масс материальных точек () (на которые следует провести разбиение рассматриваемого тела) на квадраты расстояний () от них до оси вращения:
• Подробнее о моменте инерции можно прочитать в разделах «Момент инерции тела», «Момент инерции материальной точки», «Момент инерции, единицы измерения».

Закон инерции

Закон инерции, который мы знаем, сформулировал И. Ньютон: Каждое тело находится в состоянии покоя или движется равномерно и прямолинейно, относительно любой инерциальной системы отсчета, до того момента пока действие на него других тел не заставит его изменить свое состояние.

Закон инерции является важным и независимым законом. Он отображает возможность определить пригодность системы отсчета для рассмотрения движения в динамическом и кинематическом смыслах. Он стал первым шагом при установлении основных законов классической механики.

Движение по инерции является обязательно равномерным и прямолинейным.

Такое движение можно считать аналогичным покою, так как всегда можно выбрать такую инерциальную систему отсчета, которая бы перемещалась со скоростью рассматриваемого тела и в ней тело будет покоиться.

Из предисловия к четвертому изданию

Предлагаемая вниманию читателей книга представляет собой первый том учебного пособия по курсу общей физики для втузов. Автор в течение ряда лет преподавал общую физику в Московском инженерно-физическом институте. Естественно поэтому, что пособие он писал имея в виду прежде всего студентов инженерно-физических специальностей втузов.

При написании книги автор стремился познакомить учащихся с основными идеями и методами физической науки, научить их физически мыслить. Поэтому книга не является по своему характеру энциклопедичной, содержание в основном посвящено тому, чтобы разъяснить смысл физических законов и научить сознательно применять их. Не осведомленности читателя по максимально широкому кругу вопросов, а глубоких знаний фундаментальным основам физической пауки — вот что стремился добиться автор.

Тела, совершающие круговые движения, в физике принято описывать с помощью формул, включающих в себя угловую скорость и угловое ускорение, а также такие величины, как моменты вращения, сил и инерции. Рассмотрим подробнее эти понятия в статье.

Определение момента инерции

Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.

По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.

Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.

Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:

Что такое момент инерции

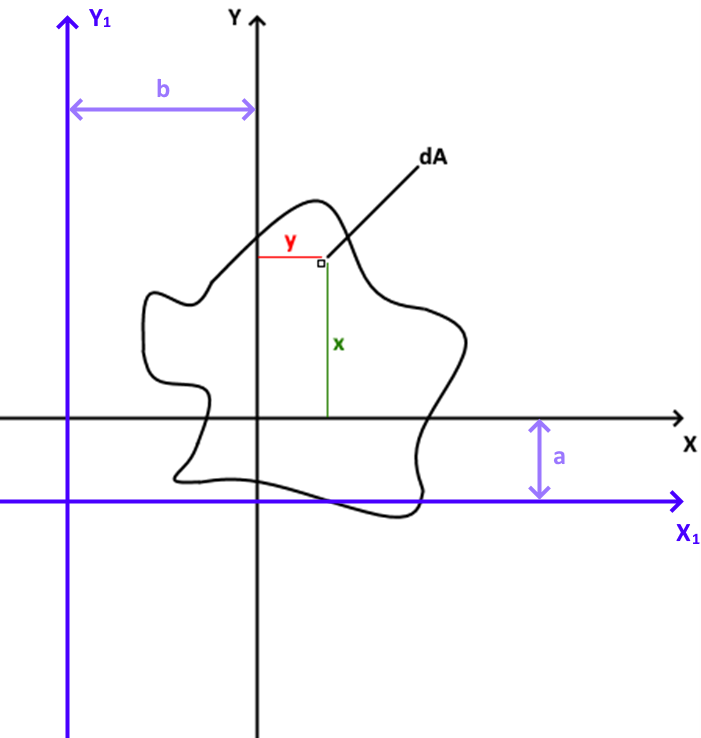Рисунок 1. Поперечное сечение стержня. Где-то я его уже видел…

Суть и смысл моментов инерции в общем случае походит на статические моменты, однако корни нужно искать в описании вращения тела. Для вращательного движения одного только значения массы тела недостаточно, требуется еще знать распределение этой массы в теле. Рассмотрим вращающееся тело, как совокупность точек с предельно малыми размером и массой, которые находятся на расстояниях Ri (от нуля до R):

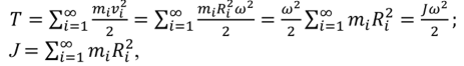Где:T — кинетическая энергия;J — момент инерции;m — масса; v — скорость; w — угловая скорость;R — радиус;

Тут видно, что также, как в формуле кинетической энергии при линейном движении мера инертности — масса, при вращательном движении мера инертности — момент инерции. Впрочем, я немного забегаю вперёд.

Угловая скорость вращающегося тела — угол поворота, пройденный за единицу времени

Тут начальный угол поворота φ может быть равен нулю, если мы рассматриваем начало движения. 

Линейная скорость тела:

где r — расстояние от рассматриваемой точки до оси вращения

Ускорение вращающегося тела (а нас интересует нормальное) тогда:

Я не буду затрагивать динамику вращающегося тела, и расскажу только о жизненно необходимом.

Сила (которая по второму закону Ньютона — произведение массы на ускорение):

и момент:

И вот тут вспомним уже третий закон Ньютона — действию всегда есть равное и противоположное противодействие, а значит действию найденного нами момента будет сопротивляться — момент инерции.

Вспомним также, что, как и со статическими моментами, на разные точки тела, удаленные от оси вращения на разные расстояния будет действовать разный момент, а общий момент можно получить их просуммировав:

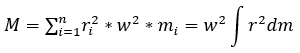
При этом значения вращающего момента и момента инерции будут равны, а сами моменты направлены в противоположные стороны. При постоянной угловой скорости вращения, например w = 1, основными величинами, характеризующими вращающий момент или момент инерции будут масса материальных точек, составляющих тело, и расстояния от этих точек до оси вращения. Но, как я уже показал, рассказывая про статические моменты, массу точек для изотропных (в данном случае имеющих одинаковую плотность) объектов можно выносить за скобки и рассматривать исключительно геометрию. Формула момента инерции примет следующий вид:

Почему I_р? Потому что мы с вами оперировали радиусом и углом поворота (в формуле угловой скорости) — т.е. использовали полярную систему отсчета (что и демонстрирует индекс p).

Таким образом момент инерции является мерой инертности тела при вращательном движении, подобно тому как масса является мерой инертности тела при поступательном прямолинейном движении.

ПРАКТИЧЕСКАЯ ЧАСТЬ

Задание 1. Определение момента инерции диска

1. Снимите дополнительные грузы с диска.

2. Измерьте штангенциркулем диаметр шкива d в нескольких местах, записы­вая результаты в табл. 1, и определите его среднее значение.

Студенческие работы

Таблица 1

№ п. п.	d, м	t, с	h, м	r = d / 2 = м m = кг h0 = м
1
2
3
4
5
Среднее значение				Jд = кг м2

3. Вращая диск, намотайте нить в один слой на шкив и включите электромаг­нит красной кнопкой, расположенной в верхней части установки. Измерьте и запишите расстояние h0 от груза до нулевой отметки шкалы.

4. Определите массу груза m, подвешенного к нити, включите секундомер.

5. В момент прохождения грузом нижнего положения секундомер выключает­ся. Продолжая дальше наблюдение за движением груза m, заметьте высоту h, на которую поднимется груз, двигаясь по инерции. Показание секундомера t и вы­соту h запишите в табл. 1.

6. Повторите измерения еще четыре раза при тех же значениях m и h0.

7. Вычислите среднее значение момента инерции диска IД по формуле (9).

Задание 2. Проверка теоремы Штейнера

1. Определите массу m0 и радиус R дополнительных грузов. Закрепите их на одинаковом расстоянии от оси вращения на диске установки и замерьте рас­стояние l1 от оси вращения до центра грузов. Результаты этих измерений и чис­ло дополнительных грузов к занесите в табл. 2.

m0 = кг k = R = м r = м h0 = м IД = кг м2	№ п. п.	l1= м	l2= м	l3= м	l4= м
t, с	h, м	t, с	h, м	t, с	h, м	t, с	h, м
1
2
3
4
5
Среднее
Jэкспер

2. Занесите в табл. 2 результаты измерений, полученных в задании 1: радиус шкива r, массу груза m, расстояние, проходимое грузом до нулевой отметки h0, момент инерции диска JД и число дополнительных грузов к.

3. Проведите измерения (см. пп. 2-6 задания 1) и результаты занесите в табл.2.

4. Рассчитайте момент инерции Jэкспер диска с дополнительными грузами (формула 9).

5. Рассчитайте момент инерции дополнительных грузов JГ, используя теорему Штейнера и результат занесите в табл.2.

6. Рассчитайте момент инерции системы «диск-дополнительные грузы» Jрасч = JД + k JГ

7. Проведите подобные измерения и расчеты с другим положением допол­нительных грузов на диске (пп. 3-6 задания1).

8. Сравните полученное экспериментально значение момента инерции Jэкспер и расчетное значение момента инерции системы Jрасч и сделайте выводы.

9. Оцените погрешность измерения. Сравните расчетные значения момента инерции и полученные экспери­ментально и сделайте выводы.

ВОПРОСЫ К ДОПУСКУ

1.  Чему равен момент инерции материальной точки?

2.  От каких величин зависит момент инерции диска?

3.  Чему равен момент инерции твёрдого тела относительно оси?

4.  В каких единицах измеряют момент инерции?

5.  Чему равен момент инерции системы тел относительно какой-то оси?

6.  Запишите закон сохранения энергии для системы «диск—груз».

7.  На что расходуется механическая энергия в системе:

а) потенциальная энергия груза при его опускании;

б) кинетическая энергия системы при движении груза вверх?

8.  Какое положение груза соответствует наибольшей кинетической энергии маховика?

9.  По какой формуле определяют работу, затраченную на преодоление сил трения?

10.  Чему равна работа постоянного момента силы?

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. В чем состоит метод определения момента инерции диска в данной работе? По какой формуле его рассчитывают в опытах?

2. Чем обусловлена погрешность в данной работе?

3. От каких величин зависит кинетическая энергия тела при поступательном и вращательном движениях?

4. Что характеризует момент инерции материальной точки, тела?

5. От каких величин зависит момент инерции тела?

6. Сформулируйте и докажите теорему Штейнера.

7. Как рассчитывают момент инерции твёрдого тела сложной формы?

8. Найти момент инерции однородной пирамиды, основанием которой служит квадрат со стороной a, относительно оси, проходящей через вершину и центр основания. Масса пирамиды равна m.

9. Две материальные точки с массами m1 и m2 соединены жестким невесомым стержнем длины l. Найти момент инерции этой системы относительно перпендикулярной к стержню оси, проходящей через центр масс.

Закон сохранения величины L

Изменение момента вращения во времени описывается приведенной ниже формулой:

Здесь M — это момент результирующей внешней силы F, приложенной к плечу r относительно оси вращения.

Формула показывает, если M=0, тогда изменение момента импульса L не будет происходить, то есть он будет оставаться сколь угодно длительное время неизменным независимо от внутренних изменений в системе. Этот случай записывают в виде выражения:

То есть любые изменения внутри системы момента I будут приводить к изменениям угловой скорости ω таким образом, что их произведение будет оставаться постоянным.

Примером проявления этого закона является спортсмен в фигурном катании, который, выбрасывая руки и прижимая их к телу, меняет свой I, что отражается на изменении его скорости вращения ω.

Задача на вращение Земли вокруг Солнца

Решим одну интересную задачу: используя приведенные выше формулы, необходимо рассчитать момент вращения нашей планеты по своей орбите.

Поскольку притяжением остальных планет можно пренебречь, а также учитывая, что момент гравитационной силы, действующей со стороны Солнца на Землю, равен нулю (плечо r=0), то L=const. Для вычисления L воспользуемся следующими выражениями:

Здесь мы приняли, что Землю можно считать материальной точкой с массой m=5,972*1024 кг, поскольку ее размеры намного меньше расстояния до Солнца r=149,6 млн км. T = 365,256 дня — период обращения планеты вокруг своей звезды (1 год). Подставляя все данные в выражение выше, получаем :

Рассчитанное значение момента импульса является гигантским, что обусловлено большой массой планеты, высокой скоростью ее вращения по орбите и огромным астрономическим расстоянием.

МОМЕНТОМ ИНЕРЦИИ I тела относительно точки, оси или плоскости называется сумма произведений массы точек тела mi, на квадраты их расстояний ri до точки, оси или плоскости: Момент .

Теорема Гюйгенса — Штейнера

Теорема была названа в честь двух математиков, давших формулировку определению характеристики параллельных осей. Например, пусть имеется объект произвольной формы, центробежная сила которого известна. Используя формулу Штейнера, можно вычислить момент тела относительно любой оси параллельной линии, проходящей через середину фигуры. В своём выводе учёные опирались на две формулы:

1. Вычисления координаты центра масс: X = (m1*x1 + m2*x2+…+Mi*Xi) / (m1+m2+…+Mi) = (Σ Δ mi*ri 2)/ m.
2. Универсального расчёта инерции любого тела: I = Σ Δ mi*ri 2.

Обозначив центр произвольной оси буквой O, а один из множества кусков — Δm, можно воспользоваться универсальной формулой. Сначала необходимо определить квадрат расстояния до оси вращения ri. Для этого через центр проведём ось Oц, а расстояние между O и Oц обозначим как d.

Указанные значения нужно выразить через координаты кусочка. Для этого строится ось абсциссы, проходящая через Oц, и ординаты — O. При таком выборе направления начала координат x центр масс равняется d, а у — нулю. Фактически получится прямоугольный треугольник. Воспользовавшись теоремой Пифагора, можно записать: I = Σ Δ mi* (xi2 + yi2).

В результате можно отметить, что момент в точке O будет прямо пропорционален расстоянию между Δ m и центром. Это и есть главный вектор на чертеже. Для его обозначения вводится длина r’.

Находится ri’2 по формулам для прямоугольного треугольника, в котором один катет равняется yi, а другой — xi — Oц. Значение ri’ совпадает с длиной гипотенузы. Таким образом, ri’2 = (xi — Oц)2 + yi2. Подставив полученное равенство в формулу нахождения параметра момента в центре, можно получить следующую формулу: Io = Σ Δ mi* ((xi — Oц)2 + yi2). После ряда подстановок и упрощения выражения в итоге получится равенство Io = I + m*x i2 — 2*m*xi2 = I — m*xi2.

Так как x центра масс совпадает с d, расстоянием между осями, одну из которых можно направить через центр, то формулу можно переписать как Io = I — m*d2. Выразив из выражения произвольный момент, формула Штейнера примет вид I = Io + m*d2.

Другими словами, теорема определяет, что характеристика инерции тела относительно любой оси находится как сумма моментов относительно параллельной оси, пересекающей центр масс, и произведению массы тела на квадрат расстояния между осями. Сопротивлением вращению пренебрегают.

Примеры решения задач

Применение на практике приведенных формул происходит, например, для решения следующих задач.

Пример №1

Задано найти МИ однородного диска с известными массой и радиусом. Из дополнительных сведений: ось вращения – через центр диска.

Для решения диск разбивается на тонкие кольца, радиусы которых равняются от 0 до R. Взяв одно из них и обозначив его радиус буквой \(r\), а массу – \(dm\), формула для расчета МИ  (согласно теореме Гюйгенса-Штейнера) выглядит следующим образом: \(dJ=dmr2.\)

С учетом подстановки в конечную формулу для определения МИ формулы для массы кольца получаем:

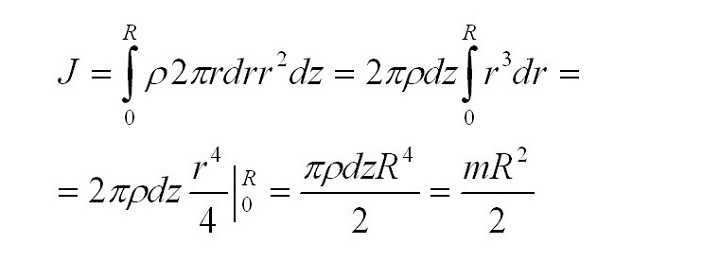
Пример № 2

Задано найти у того же диска МИ относительно оси, которая проходит через середину радиуса.

Из предшествующего задания используем найденную величину МИ относительно оси, которая проходит через центр масс. Используя формулу Штейнера, решаем задачу.